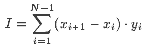 ):
):- pro funkci zadanou tabulkou (využijeme všechny zadané body [xi,yi]) a
- pro funkci, jejíž analytické vyjáření známe (zde si vybereme N uzlových bodů).
fevalFunkce feval se používá v případě, kdy potřebujeme
vyhodnotit (zavolat) existující funkci, ale předem nevíme, jak se
volaná funkce bude jmenovat. Nejčastěji je to v případě, kdy vytváříme
nějaký univerzální nástroj, např. pro hledání kořenů nějaké funkce nebo
pro výpočet určitého integrálu nějaké funkce v daném intervalu.
Syntaxe:
[y1,y2,...] = feval(fhandle,x1,...,xn) nebo
[y1,y2,...] = feval(funkce,x1,...,xn)
handle je "ukazatel" na funkcifunkce je řetězec obsahující název volané funkcex1,...,xn jsou všechny vstupní parametry volané funkcey1,y2,... jsou odebírané výstupy
Následujících 5 zápisů je ekvivalentních:
y = sin(x)
y = feval(@sin,x)
y = feval('sin',x)
nazev='sin'; y = feval(nazev,x)
fhand=@sin; y = feval(fhand,x)
Poznámka: funkce volaná pomocí feval musí být buď knihovní funkcí MATLABu, anebo uživatelskou funkcí uloženou v M-souboru (nejlépe v aktuálním adresáři).
Příklad:
máme funkci polynom1 uloženou v souboru polynom1.m, která má jeden vstup a jeden výstup:
polynom1.m |
function v=polynom1(u) % polynom1 - funkcni hodnoty polynomu 3. stupne v = 2*u.^3 - u.^2 + 15*u -8; % funguje i pro vektory nebo matice (po prvcích) |
y = polynom1(30.2)
y = feval(@polynom1,-13)
y = feval('polynom1',-4.5)
nazev='polynom1'; x=5.21; y = feval(nazev,x)
fhand=@polynom1; x=7/4-0.5; y = feval(fhand,x)
Další příklady použití funkce feval naleznete níže.
Potřebujeme-li vypočítat určitý integrál, ale:
My si uvedeme dvě možnosti realizace obdélníkového pravidla (použijeme náhradu určitého integrálu součtem 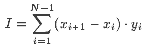 ):
):
- pro funkci zadanou tabulkou (využijeme všechny zadané body [xi,yi]) a
- pro funkci, jejíž analytické vyjáření známe (zde si vybereme N uzlových bodů).
integ_obd.m |
function I=integ_obd(x,y)
% integ_obd - urcity integral (obdelnikove pravidlo), funkce je zadana tabulkou
% I=integ_obd(x,y)
% x ... vektor hodnot nezavisle promenne (delka N)
% y ... vektor funkcnich hodnot (delka N)
% I ... priblizna hodnota integralu
% priklad: x=0:pi/100:pi; I=integ_obd(x,sin(x))
N=length(x);
if N~=length(y) % kdyby nebylo x a y stejne dlouhe
error('Vstupni vektory maji ruznou delku!')
end
if N<2
error('Pro vypocet potrebuji alespon DVA body!')
end
I = 0; % priprava
for i=1:N-1
I = I + (x(i+1)-x(i))*y(i); % pridani 1 obdelniku
end
|
Následující funkce vrací hodnotu určitého integrálu od a do b pro libovolnou funkci jednné proměnné (tato funkce je zadána svým názvem a pro zjištění jejích funkčních hodnot se používá feval).
integ_obd_fce.m |
function I=integ_obd_fce(a,b,N,nazevfce)
% integ_obd_fce - urcity integral (obdelnikove pravidlo), funkce je znama
% I=integ_obd_fce(a,b,N,nazevfce)
% a ... dolni mez
% b ... horni mez
% N ... pocet dilku
% nazevfce ... retezec: nazev existujici funkce (tj. je ulozena v M-souboru)
% I ... priblizna hodnota integralu
% priklad: I=integ_obd_fce(0,pi,100,'sin')
if a>=b
error('Chybne zadane meze!')
end
if N<1
error('Pocet dilku musi byt kladny!')
end
h = (b-a)/N; % krok
I = 0; % priprava
for i=a:h:b
y = feval(nazevfce,i); % zjisteni funkcni hodnoty v bode 'i'
I = I + h*y; % pridani 1 obdelniku
end
|
Pokud máme k dispozici tzv. symbolický toolbox, můžeme MATLAB využít pro přesné výpočty určitých integrálů (pokud existují) nebo pro nalezení primitivní funkce (existuje-li).
Postup je jednoduchý:
syms proměnná1 proměnná2 proměnná3
int(výraz,a,b), kde výraz musí obsahovat některou existující symbolickou proměnnou. Funkce int vrací jeden výstup, který můžeme uložit do nějaké proměnné
int s jedním parametrem:int(výraz)
pretty(symb_výraz)
Příklad 1 - určité integrály polynomů:
>> syms x ... všimněte si, jak se zobrazuje symbolická proměnná v okénku Workspace
>> int(x^2+3*x-5,0,2) ... ve výrazech se symbolickou proměnnou lze použít všechny známé aritmetické operátory
ans = ... všimněte si, že výsledkem je zase symbolická proměnná
-4/3
>> int(polynom1(x),0,2) ... symbolickou proměnnou lze poslat do existující funkce
ans =
58/3
Příklad 2 - primitivní funkce:
>> syms x
>> int(x^2+3*x-5)
ans =
1/3*x^3+3/2*x^2-5*x
>> int(polynom1(x))
ans =
1/2*x^4-1/3*x^3+15/2*x^2-8*x
>> pretty(int(polynom1(x))) ... hezké zobrazení výsledku (totéž jako pretty(ans))
4 3 2
1/2 x - 1/3 x + 15/2 x - 8 x
V případě, že určitý integrál existuje, můžeme symbolickou matematiku použít při ověřování výsledků získaných numericky.
VÝPOČET URČ. INTEGRÁLU OBĚMA ZPŮSOBY - pracuje se na tom...
Častou úlohou je odhadnout derivaci funkce f v bodě c, tj. hodnotu f'(c), na základě znalosti funkčních hodnot v konečně mnoha bodech. Tyto body si buď můžeme zvolit, anebo jsou zadány (např. tabulkou).
Většinou nic nebrání tomu, abychom aproximovali f nějakou vhodnou funkcí, tuto funkci zderivovali a výsledek považovali za aproximaci derivace původní funkce.
Provést odhad derivace je žádoucí, pokud je analytický výpočet derivace
příliš pracný nebo popis funkce je tak složitý, že bychom se do jeho
derivování nechtěli pouštet (třeba kvůli riziku chyby).
Numerická derivace však může být také nežádoucí - chyba derivace
nesouvisí s chybou, která vznikla při aproximaci dané funkce, a může
být tedy libovolně velká.
Při odhadu derivace funkce f můžeme vyjít z definice:
f'(x) = limh![]() 0 (f(x+h) - f(x))/h,
kde h je z prstencového okolí nuly. Zvolíme-li "malé" h, dostaneme odhad derivace v bodě x.
0 (f(x+h) - f(x))/h,
kde h je z prstencového okolí nuly. Zvolíme-li "malé" h, dostaneme odhad derivace v bodě x.
Tento postup nelze použít u funkcí zadaných tabulkou (kdy neznáme analytické vyjádření funkce).
Dále můžeme pro výpočet numerické derivace použít následujících aproximací funkcí: interpolačního spline, aproximace pomocí Čebyševových polynomů, aproximace metodou nejmenších čtverců (u derivací funkce dané naměřenými hodnotami), interpolační polynom.
Pokud je funkce zadaná tabulkou, přičemž vzdálenosti hodnot x1,...,xn
jsou ekvidistantní, můžeme použít interpolaci polynomem 2. stupně a
získáme vztahy pro výpočet derivace v daných bodech - derivaci (tj.
směrnici tečny ke grafu funkce) ve vnitřních bodech x2,...,xn-1 určíme podle symetrického vzorce a okraje dopočítáme z bodů uvnitř:
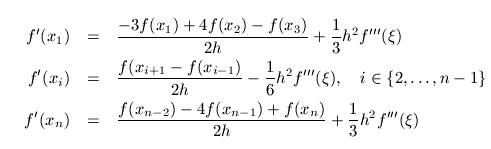
Poznámka: abychom docílili malou chybu metody, potřebujeme
volit malý krok. V tom případe však v čitateli vzorce dostáváme malý
rozdíl čísel, který poté dělíme malým jmenovatelem. Takto může pro malý
krok vzniknout velká zaokrouhlovací chyba. Proto není vhodné volit krok
příliš malý.
Následující funkce vrací vektor hodnot derivace funkce zadané tabulkou.
derivace.m |
function dy=derivace(x,y)
% DERIVACE - numericka derivace funkce dane tabulkou
% dy=derivace(x,y)
% x ... vektor hodnot nezavisle promenne, ekvidistantni (delka N)
% y ... vektor funkcnich hodnot (delka N)
% dy ... vektor pribliznych hodnot derivace v bodech [xi,yi] (delka N)
N = length(x);
if N~=length(y)
error('Vstupni vektory nejsou stejne dlouhe!')
end
if N<3
error('Zadali jste malo bodu - potrebuji alespon TRI hodnoty!')
end
h = (x(2)-x(1)); % krok
%...melo by se oTESTovat, ze krok je vsude stejny!...
dy = y; % priprava, 'dy' je stejne velke jako 'y'
% zmena hodnot 'dy' na spravne:
dy(1) = (-3*y(1)+4*y(2)-y(3))/(2*h); % pocatek
for i=2:N-1
dy(i) = (y(i+1)-y(i-1))/(2*h); % vnitrni body
end
dy(N) = (y(N-2)-4*y(N-1)+3*y(N))/(2*h); % konec
|
Příklad:
Funkci vyzkoušíme pro parabolu (tam by se numerická derivace měla
shodovat s analytickou), přičemž zvolíme krok 1/5 a necháme vykreslit
graf původní funkce (černě), její derivace (zeleně) a numericky
spočítané derivace (červené křížky):
>> x=-2:0.2:2; y=x.^2; dy=derivace(x,y); plot(x,y,'k',x,2*x,'g',x,dy,'rx')
a také vyzkoušíme pro "polynom1" (barvy grafů jsou stejné jako v předešlém případě, grafy nejsou popsány!):
>> x=-2:0.2:2; dy=derivace(x,polynom1(x)); % numericka derivace
>> ady = 6*x.^2-2*x+15; % analyticka derivace
>> plot(x,y,'k',x,ady,'g',x,dy,'rx')
Pokud máme k dispozici tzv. symbolický toolbox, můžeme MATLAB využít pro výpočet derivace dané funkce (výrazu).
Postup je jednoduchý:
syms proměnná
diff(výraz), kde výraz musí obsahovat symbolickou proměnnou. Výstup funkce je jeden - hledaná derivace (můžeme ji uložit do proměnné)
diff se dvěma parametry, tj. diff(výraz,n, kde n>1 je řád derivace
ezplot(x,y), kde x je symbolická proměnná a y je původní funkce nebo její derivace
pretty(symb_výraz)
subs(symb_výraz,stare,nove), kde stare je výraz (proměnná), za který dosazujeme a nove je výraz (proměnná), kterým nahrazujeme
Příklad 1 - derivace polynomu a vykreslení dvou grafů do jednoho obrázku:
>> syms x
>> y = x^2+3*x-5;
>> dy = diff(y)
>> ezplot(x,y) graf fce
>> hold on % prikreslujeme
>> ezplot(x,dy) graf derivace
Poznámka: graf by se měl také správně popsat (xlabel, title, legend)!
Příklad 2 - první, druhá a třetí derivace funkce sin(x2):
>> syms x
>> diff(sin(x^2)) % 1. derivace
ans =
2*cos(x^2)*x
>> diff(sin(x^2),2) % 2. derivace
ans =
-4*sin(x^2)*x^2+2*cos(x^2)
>> diff(sin(x^2),3) % 3. derivace
ans =
-8*cos(x^2)*x^3-12*sin(x^2)*x
>> pretty(diff(sin(x^2),3)) % hezky vypis
2 3 2
-8 cos(x ) x - 12 sin(x ) x
Symbolicky určenou derivaci lze použít k ověření výsledků nalezených numericky, pokud známe analytické vyjádření původní funkce.
Příklad 3 - ověření numerického výpočtu derivace funkce "polynom1" pomocí symb. matematiky:
>> x=-2:0.2:2; dy=derivace(x,polynom1(x)); % numericka derivace
>> syms z; ady = subs(diff(polynom1(z)),z,x); % symb. derivace + dosazeni hodnot 'x' za 'z'
>> plot(x,y,'k',x,ady,'g',x,dy,'rx')
Postup je následující:
 Možnosti,
karta Mezinárodní). Není-li v menu Excelu tato možnost, musíme změnit
desetinnou čárku na tečku pro všechny aplikace (Start
Možnosti,
karta Mezinárodní). Není-li v menu Excelu tato možnost, musíme změnit
desetinnou čárku na tečku pro všechny aplikace (Start Nastavení
Nastavení Ovládací panely, kde na kartě Čísla změníme oddělovač).
Ovládací panely, kde na kartě Čísla změníme oddělovač).
ddeinit)>> spojeni=ddeinit('excel','data1.xls')spojeni přesně nula, spojení se nepovedlo (pravděpodobně není otevřen soubor uvedeného názvu).
ddereq)>> x=ddereq(spojeni,'r1c1:r21c1'),
kde 'r1c1:r21c1' znamená, že bereme data od buňky v 1. řádku a 1.
sloupci do buňky v 21. řádku a 1. sloupci (tedy od A1 do A21).