3D grafika

V lekci 5 jsme se seznámili s 2D grafikou (grafy funkcí jedné proměnné). MATLAB umožňuje vizualizovat také funkce dvou proměnných. Používáme podobný postup:

  1. příprava dat (nezávisle proměnné, závisle proměnná)
  2. výběr grafického okna, případně podokna (lekce 5!)
  3. vykreslení 3D grafu
  4. úpravy grafu
  5. uložení grafu do souboru (lekce 5!)

Příprava dat

Potřebujeme mít dvě matice (např. X,Y), jejichž prvky X(i,j),Y(i,j) budou obsahovat souřadnice bodů v rovině. Ke snadnému generování těchto matic slouží funkce meshgrid:
[X,Y]=meshgrid(v1,v2)
- vektor v1 určuje interval na ose x s daným krokem a vektor v2 určuje interval na ose y s daným krokem
[X,Y]=meshgrid(v)
- vektor v určuje interval na ose x i na ose y

Ukázka:

>> [X,Y]=meshgrid([-3:1],[-1:2:7])

X =
    -3    -2    -1     0     1
    -3    -2    -1     0     1
    -3    -2    -1     0     1
    -3    -2    -1     0     1
    -3    -2    -1     0     1

Y =
    -1    -1    -1    -1    -1
     1     1     1     1     1
     3     3     3     3     3
     5     5     5     5     5
     7     7     7     7     7

Kromě nezávisle proměnných potřebujeme vytvořit také matici funkčních hodnot.
Např. pro funkci f(x,y)=cos(x2)-sin(y3) vytvoříme matici Z:
>> Z=cos(X.^2)-sin(Y.^3);   (uvědomte si, proč je nezbytné používat operátory "s tečkou"...)

Vykreslení grafu funkce dvou proměnných

Při vykreslení grafů funkce dvou proměnných máme na výběr:


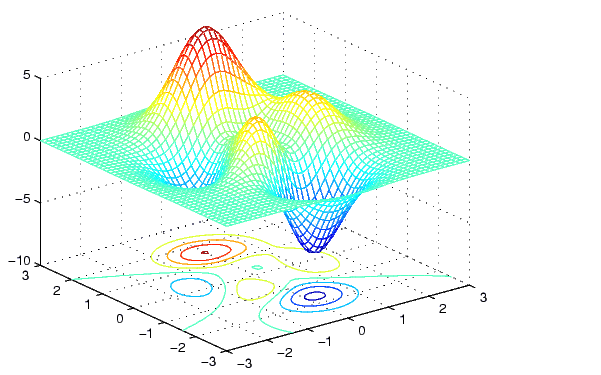
Příklad - ukázka skriptu, který vykreslí funkci dvou proměnných (funkce peaks je knihovní funkce MATLABu): 

[X,Y] = meshgrid(-3:.125:3);
Z = peaks(X,Y);
meshc(X,Y,Z);
axis([-3 3 -3 3 -10 5])

Úpravy grafu

Symbolická matematika

Dosud probrané příkazy (viz lekce8.html - symbolická integrace a symbolická derivace):
syms ... vytvoření symbolické proměnné
int ... symbolický určitý nebo neurčitý integrál (existuje-li)
pretty ... výpis symbolického výrazu "jako na papíře"
diff ... symbolická derivace
ezplot ... kreslení grafu symbolické funkce jedné proměnné
subs ... nahrazování v symbolických výrazech

Uvedeme si ještě některé užitečné symbolické funkce:

Výpočet limit

limit(výraz) ... limita výrazu, kdy symbolická proměnná (nalezená pomocí findsym) se blíží nule
limit(výraz,p,a) ... limita výrazu, kdy symbolická proměnná p se blíží k hodnotě a
limit(výraz,p,a,'left') ... limita výrazu, kdy symbolická proměnná p se blíží k hodnotě a zleva
limit(výraz,p,a,'right') ... limita výrazu, kdy symbolická proměnná p se blíží k hodnotě a zprava

Příklad: 

>> syms x

>> limit(sin(x)/x)
ans =
1

>> limit(1/x)
ans =
NaN

>> limit(1/x,x,0,'left')
ans =
-inf

>> limit(1/x,x,0,'right')
ans =
inf

>> limit(1/x+5,x,inf)
ans =
5

Symbolický součet

symsum(výraz) ... vztah pro součet od 0 do x-1, kde x je symbolická proměnná použitá ve výrazu (tato proměnná je nalezena automaticky pomocí findsym)
symsum(výraz,k) ... vztah pro součet od 0 do k-1, kde k je určená symbolická proměnná
symsum(výraz,a,b) ... vztah pro součet od a do b pro symbolickou proměnnou nalezenou automaticky
symsum(výraz,k,a,b) ... vztah pro součet od a do b pro symbolickou proměnnou k

Příklad: 

>> syms s
>> s1 = symsum(1/s^2,1,inf) % nekonečná řada
s1 =
1/6*pi^2

>> s_obec=symsum(s^2)
s_obec =
1/3*s^3-1/2*s^2+1/6*s
>> pretty(ans)
                   3        2
              1/3 s  - 1/2 s  + 1/6 s

>> s2=symsum(s^2,0,10) % 0+1+4+9+...+100
s2 =
385

>> subs(s_obec,11) % overeni 's_obec' pro prvnich 11 clenu (0-10)
ans =
   385.0000 % VŠIMNĚTE SI: výsledek už není symbolická proměnná

Symbolická kalkulačka

Příkazem funtool se spustí symbolická kalkulačka - je obsažena ve třech grafických oknech a umožňuje pracovat se dvěma symbolickými funkcemi (a současně ukazuje jejich grafy).

Nástroj pro symbolické řešení rovnic (i soustav rovnic)

Symbolická funkce solve hledá řešení rovnice (nebo soustav rovnic). Pokud nemůže být určeno symbolické řešení, funkce vrátí řešení numerické. My si uvedeme zápis funkce pro případ řešení jedné rovnice.

solve(rce) ... vypíše řešení rovnice rce, která je zadaná buď řetězcem, anebo symbolickým výrazem (kdy se rovná nule) - symbolická proměnná, pro niž se rovnice řeší, se hledá automaticky (pomocí findsym)

Příklad: 

>> syms x
>> r=solve(3*x^2-2*x-5)
r =
[  -1]
[ 5/3]
 
>> rd=double(r) % prevod symbolickeho vysledku na matici komplexnich (realnych) CISEL
rd =
   -1.0000
    1.6667

>> x=solve('3*x^2+1=2*x')
x =
[ 1/3+1/3*i*2^(1/2)]
[ 1/3-1/3*i*2^(1/2)]
 
>> xd=double(x) % prevod na cisla; 'xd' bude matice
xd =
   0.3333 + 0.4714i
   0.3333 - 0.4714i

Pokud je v symbolickém výrazu více symbolických proměnných, je vhodné zadat, pro kterou z nich hledáme řešení:
solve(rce,p) ... vypíše řešení rovnice rce pro symbolickou proměnnou p
V následujícím příkladu je nejprve vyhledání symbolické proměnné necháno na MATLABU, a pak je určeno, že chceme řešit pro proměnnou b.

Příklad: 

>> syms a b c x

>> solve('a*x^2+b*x+c=0') % reseni (kvadraticke) rovnice pro 'x'
ans =
[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))]
[ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]
>> pretty(ans)
        [           2         1/2]
        [    -b + (b  - 4 a c)   ]
        [1/2 --------------------]
        [             a          ]
        [                        ]
        [           2         1/2]
        [    -b - (b  - 4 a c)   ]
        [1/2 --------------------]
        [             a          ]

>> solve('a*x^2+b*x+c=0',b) % reseni (linearni) rovnice pro 'b'
ans =
-(a*x^2+c)/x
>> pretty(ans)
                     2
                  a x  + c
                - --------
                     x

Přehled všech symbolických funkcí získáte pomocí >> help symbolic.



Řešení nelineární rovnice v MATLABu

  1. symbolicky - solve (popsáno výše)
  2. numericky - viz internetové skriptum
  3. hledání kořenů polynomů - funkce roots
    r=roots(v) ... najde všechny kořeny polynomu, který je zadán vektorem v v pořadí od koeficientu u xn do absolutního členu (např. polynomu 5x3-2x2+4 odpovídá v=[5 -2 0 4])

    Příklad:

    >> r1=roots([5 -2 0 4])
r1 =
   0.6062 + 0.7857i
   0.6062 - 0.7857i
  -0.8123

>> % SROVNEJME:
>> r2=double(solve('5*x^3-2*x^2+4=0'))
r2 =
  -0.8123          
   0.6062 - 0.7857i
   0.6062 + 0.7857i



    Předchozí lekce   PŘEHLED   Další lekce