Helikoptéra - algoritmus stavového prediktívneho riadenia

V každom kroku výpočtu sú počítané predikované hodnoty výstupu na N₂ krokov dopredu a riadiace zásahy pre nasledujúcich N_u krokov dopredu, ako môžete vidieť na Obr. 2.

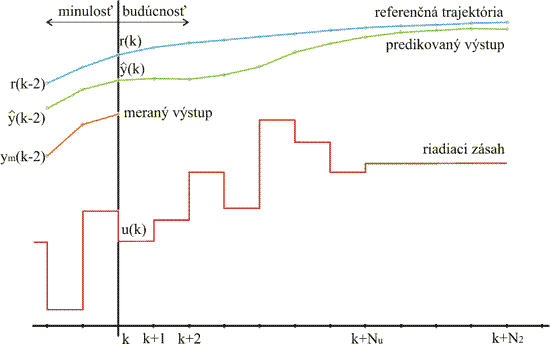
Obr. 2 Princíp prediktívneho horizontu pre systém s jedným vstupom a jedným výstupom

Kriteriálnu funkciu pre výpočet optimálneho riadenia v k-tom kroku si môžeme vyjadriť v tvare:

kde:

Pri odvodení stavového MPC regulátora pre nelineárny systém s m výstupmi a n vstupmi uvažujeme zlinearizovaný model systému v okolo pracovného prevedený do diskrétneho stavového opisu v nasledujúcom tvare:

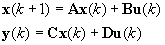
Prediktor na N_p krokov dopredu môžeme zapísať v maticovom tvare:

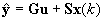
kde:

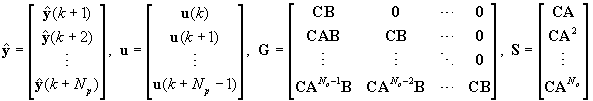
Vektor optimálnych riadiacich zásahov sa vypočita podľa vzťahu:

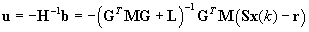
kde:

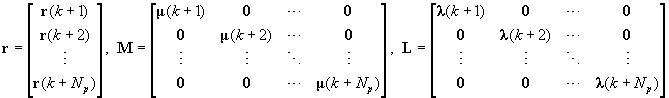
Výsledkom tejto rovnice je trajektória tvorená riadiacimi zásahmi, z ktorých prvých n prvkov vektora u je aplikovaných na proces. Pre systém s obmedzením hodnoty akčnej veličiny u(k) alebo hodnoty výstupu y(k) sa vypočítavá vektor u pomocou funkcie quadprog (Quadratic Programing) z Optimization Toolboxu jazyka Matlab.

Algoritmus výpočtu hodnoty akčného zásahu v k-tom kroku výpočtu má tvar:

1. Načítanie matíc A, B, C, D stavového modelu systému, vektora referenčných hodnôt výstupu systému r a váhových koeficientov m_i a l_l pre i=1,...,n a l=1,...,m,
2. Zostavenie váhových matíc M a L,
3. Výpočet matice silovej odozvy G a matice voľnej odozvy S,
4. Ak je požiadavka na obmedzenie u(k) alebo y(k) potom pokracuj bodom 7.,
5. Výpočet vektora predikcie akčného zásahu u podľa vyššie uvedeného vzťahu,
6. Pokračuj bodom 8.,
7. Výpočet vektora predikcie akčného zásahu u s použitím funkcie quadprog,
8. u(k) je prvých n prvkov vektora u,
9. Výpocet sa opakuje pre další krok výpoctu od bodu 1.