Modelovanie dynamického SISO systému dvoch guľových nádob v interakcii na báze neurónových sietí
Fyzikálno - matematický popis systému dvoch guľových nádob v interakcii:
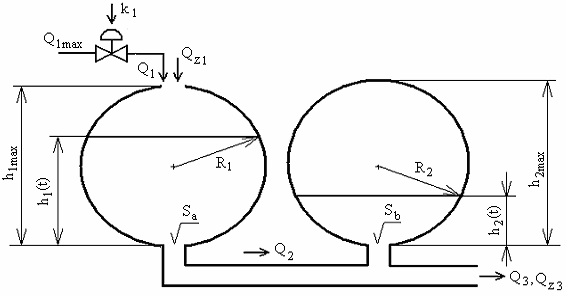
Parametre simulačného modelu:
Q1m[kg/s] - maximálny hmotnostný prítok
h1(t)[m] - výška hladiny v prvej nádobe
h2(t)[m] - výška hladiny v druhej nádobe
R1[m] - polomer prvej nádoby
R2[m] - polomer druhej nádoby
S1[m^2] - plocha hladiny v prvej nádobe
S2[m^2] - plocha hladiny v druhej nádobe
da[m] - prierez výtoku z prvej nádoby
db[m] - prierez výtoku z prvej nádoby
k1[-] - konštanta pootvorenia ventilu
Vstupná veličina:
otvorenie ventilu - k1(t)[-] v rozsahu <0, 1>
Výstupná veličina:
výška hladiny v druhej nádobe - h2(t) [m]
Poruchové veličiny:
Qz1[m^3/s], Qz2[m^3/s]
Dynamiku systému popisujú nelineárne diferenciálne rovnice:
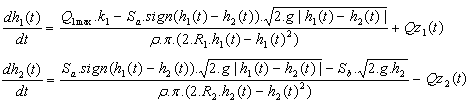
Implementácia do jazyka MATLAB/Simulink:
Nelineárne diferneciálne rovnice sú narogramované v S-funkcii, ktorá predstavuje simulačný model systému dvoch guľových nádob v interakcii.
- časť zdrojového kódu S-funkcie:

Postup experimentálnej identifikácie dynamických systémov na báze neurónových sietí typu MLP:
- Získanie trénovacích dát (realizácia experimentu)
- Voľba topológie neurónovej siete
- Trénovanie neurónovej siete
- Validácia dopredného neurónového modelu
- Ak model vyhovuje, skok na krok 6, ak nevyhovuje, skok na krok 3, 2 alebo 1
- Koniec (model vyhovujúcej kvality)
Principiálna bloková schéma pre trénovanie neurónového modelu:

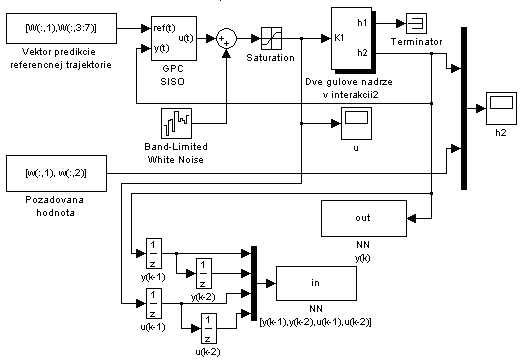
Simulačná schéma pre získavanie trénovacích dát:
Uvedená simulačná schéma slúži na získanie trénovacích dát zo simulačného modelu dvoch guľových nádob v interakcii pre trénovanie neuróho modelu:
Simulačná schéma pre overenie natrénovaného neurónového modelu (validácia):
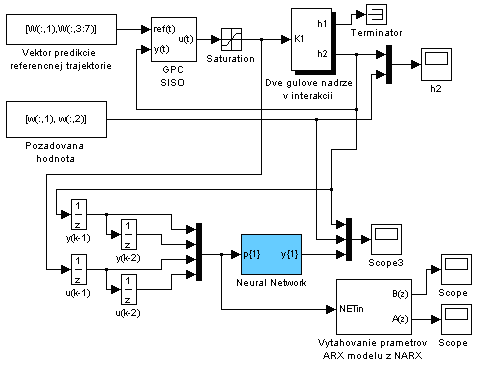
Dopredný model bude využitý v algoritme zovšeobecneného prediktívneho riadenia na nelinearny systém v cvičení 12.
|